Ułamki - doprowadzanie do wspólnego mianownika
Wypróbuj też:
Tutaj możesz zobaczyć działania prowadzące do doprawadzenia ułamków do wspólnego mianownika.
Podaj licznik i mianownik obu ułamków a następnie wciśnij przycisk Oblicz.
Porada: Licznik i mianownik nie muszą być liczbami całkowitymi, możesz używać zmiennych i wyrażeń, np: wpisz 2*x+1 dla 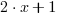
Jak to się robi?
Doprowadzanie do wspólnego mianownika
Dwa ułamki musimy doprowadzić do wspólnego mianownika zazwyczaj gdy chcemy je dodać lub odjąć a ułamki te mają różne mianowniki. Naszym celem jest wtedy wykonać takie działania, aby oba ułamki miały dokładnie tą samą liczbę (lub wyrażenie) w mianowniku, czyli pod kreską ułamkową.
Najprostszym sposobem jest pomnożenie licznika i mianownika pierwszego ułamka przez mianownik drugiego ułamka, oraz pomnożenie licznika i mianownika drugiego ułamka przez mianownik pierwszego ułamka.
Przykład:
Chcemy doprowadzić do wsólnego mianownika ułamki i
i
 . Mnożymy więc licznik i mianownik pierwszego ułamka przez
3, oraz licznik i mianownik drugiego ułamka przez 2. Otrzymujemy:
. Mnożymy więc licznik i mianownik pierwszego ułamka przez
3, oraz licznik i mianownik drugiego ułamka przez 2. Otrzymujemy:
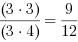 i
i 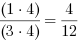
Parą ułamków doprowadzonych do wspólnego mianownika jest: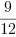 i
i
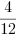 .
.
Postępowanie opisane powyżej zawsze da nam poprawny wynik, jednak czasem spowoduje, że otrzymany wspólny mianownownik nie będzie liczbą najmniejszą z możliwych. Aby otrzymać najmiejszy z możliwych mianowników mnożymy liczniki i mianowniki ułamków przez taką liczbę, aby mianownik pomnożony przez nią dał jako wynik najmniejszą wspólną wielokrotność mianowników obu ułamków (Najmniejsza wspólna wielokrotność liczb i
i 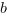 to
najmniejsza taka liczba, która jest podzielna przez zarówno przez
to
najmniejsza taka liczba, która jest podzielna przez zarówno przez  jak i przez
jak i przez 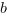 ). Najmniejsza wspólna wielokrotność mianowników obu
ułamków będzie naszym wspólnym mianownikiem. Pierwszym krokiem jest zatem jej znalezienie.
). Najmniejsza wspólna wielokrotność mianowników obu
ułamków będzie naszym wspólnym mianownikiem. Pierwszym krokiem jest zatem jej znalezienie.
Przykład:
Chcemy doprowadzić do wspólnego mianownika ułamki i
i
 . Szukamy najmniejszej wspólnej wielokrotności liczb 2 i 6.
Taką liczbą jest 6. Będzie to więc wspólny mianownik obu ułamków. Mnożymy więc licznik i mianownik
pierwszego ułamka przez taką liczbę, żeby w mianowniku dostać 6. Mamy:
. Szukamy najmniejszej wspólnej wielokrotności liczb 2 i 6.
Taką liczbą jest 6. Będzie to więc wspólny mianownik obu ułamków. Mnożymy więc licznik i mianownik
pierwszego ułamka przez taką liczbę, żeby w mianowniku dostać 6. Mamy:
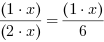
Łatwo obliczyć, że w tym wypadku x = 3. Dostajemy więc .
W drugim ułamku mianownik jest już równy 6, więc cały ułamek pozostaje bez zmian (mnożylibyśmy licznik
i mianownik przez 1, co nie zmienia wartości). Para ułamków doprowadzonych do wpólnego mianownika to:
.
W drugim ułamku mianownik jest już równy 6, więc cały ułamek pozostaje bez zmian (mnożylibyśmy licznik
i mianownik przez 1, co nie zmienia wartości). Para ułamków doprowadzonych do wpólnego mianownika to:
 i
i  . Zauważmy, że gdybyśmy
zastosowali pierwszy z omówionych sposobów wtedy mnożylibyśmy licznik i mianownik pierwszego ułameka przez 6
a drugiego przez 2 i wspólny mianownik wynosiłby 12. Wynik też byłby poprawny ale w licznikach i mianownikach
mielibyśmy większe liczby.
. Zauważmy, że gdybyśmy
zastosowali pierwszy z omówionych sposobów wtedy mnożylibyśmy licznik i mianownik pierwszego ułameka przez 6
a drugiego przez 2 i wspólny mianownik wynosiłby 12. Wynik też byłby poprawny ale w licznikach i mianownikach
mielibyśmy większe liczby.
Dwa ułamki musimy doprowadzić do wspólnego mianownika zazwyczaj gdy chcemy je dodać lub odjąć a ułamki te mają różne mianowniki. Naszym celem jest wtedy wykonać takie działania, aby oba ułamki miały dokładnie tą samą liczbę (lub wyrażenie) w mianowniku, czyli pod kreską ułamkową.
Najprostszym sposobem jest pomnożenie licznika i mianownika pierwszego ułamka przez mianownik drugiego ułamka, oraz pomnożenie licznika i mianownika drugiego ułamka przez mianownik pierwszego ułamka.
Przykład:
Chcemy doprowadzić do wsólnego mianownika ułamki
 i
i
 . Mnożymy więc licznik i mianownik pierwszego ułamka przez
3, oraz licznik i mianownik drugiego ułamka przez 2. Otrzymujemy:
. Mnożymy więc licznik i mianownik pierwszego ułamka przez
3, oraz licznik i mianownik drugiego ułamka przez 2. Otrzymujemy: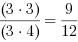 i
i 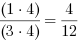
Parą ułamków doprowadzonych do wspólnego mianownika jest:
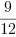 i
i
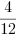 .
.Postępowanie opisane powyżej zawsze da nam poprawny wynik, jednak czasem spowoduje, że otrzymany wspólny mianownownik nie będzie liczbą najmniejszą z możliwych. Aby otrzymać najmiejszy z możliwych mianowników mnożymy liczniki i mianowniki ułamków przez taką liczbę, aby mianownik pomnożony przez nią dał jako wynik najmniejszą wspólną wielokrotność mianowników obu ułamków (Najmniejsza wspólna wielokrotność liczb
 i
i 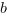 to
najmniejsza taka liczba, która jest podzielna przez zarówno przez
to
najmniejsza taka liczba, która jest podzielna przez zarówno przez  jak i przez
jak i przez 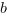 ). Najmniejsza wspólna wielokrotność mianowników obu
ułamków będzie naszym wspólnym mianownikiem. Pierwszym krokiem jest zatem jej znalezienie.
). Najmniejsza wspólna wielokrotność mianowników obu
ułamków będzie naszym wspólnym mianownikiem. Pierwszym krokiem jest zatem jej znalezienie.Przykład:
Chcemy doprowadzić do wspólnego mianownika ułamki
 i
i
 . Szukamy najmniejszej wspólnej wielokrotności liczb 2 i 6.
Taką liczbą jest 6. Będzie to więc wspólny mianownik obu ułamków. Mnożymy więc licznik i mianownik
pierwszego ułamka przez taką liczbę, żeby w mianowniku dostać 6. Mamy:
. Szukamy najmniejszej wspólnej wielokrotności liczb 2 i 6.
Taką liczbą jest 6. Będzie to więc wspólny mianownik obu ułamków. Mnożymy więc licznik i mianownik
pierwszego ułamka przez taką liczbę, żeby w mianowniku dostać 6. Mamy: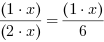
Łatwo obliczyć, że w tym wypadku x = 3. Dostajemy więc
 .
W drugim ułamku mianownik jest już równy 6, więc cały ułamek pozostaje bez zmian (mnożylibyśmy licznik
i mianownik przez 1, co nie zmienia wartości). Para ułamków doprowadzonych do wpólnego mianownika to:
.
W drugim ułamku mianownik jest już równy 6, więc cały ułamek pozostaje bez zmian (mnożylibyśmy licznik
i mianownik przez 1, co nie zmienia wartości). Para ułamków doprowadzonych do wpólnego mianownika to:
 i
i  . Zauważmy, że gdybyśmy
zastosowali pierwszy z omówionych sposobów wtedy mnożylibyśmy licznik i mianownik pierwszego ułameka przez 6
a drugiego przez 2 i wspólny mianownik wynosiłby 12. Wynik też byłby poprawny ale w licznikach i mianownikach
mielibyśmy większe liczby.
. Zauważmy, że gdybyśmy
zastosowali pierwszy z omówionych sposobów wtedy mnożylibyśmy licznik i mianownik pierwszego ułameka przez 6
a drugiego przez 2 i wspólny mianownik wynosiłby 12. Wynik też byłby poprawny ale w licznikach i mianownikach
mielibyśmy większe liczby.