Podstawy
Literały
W matematyce często reprezentujemy liczby za pomocą liter. Używamy liter
 ,
, 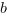 ,
,  ,
, 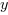 itd., mając na myśli jakieś konkretne liczby.
Wartość tych liczb jest dla nas znana lub nie, w zależności od zadania, które
w danym momencie jest rozwiązywane.
itd., mając na myśli jakieś konkretne liczby.
Wartość tych liczb jest dla nas znana lub nie, w zależności od zadania, które
w danym momencie jest rozwiązywane.
Kiedy liczba jest reprezentowana przez literę, nazywamy ją literałem,
w odróżnieniu od danych, takich jak 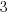 ,
, 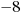 , które są zapisywane
za pomocą cyfr arabskich.
, które są zapisywane
za pomocą cyfr arabskich.
Zgodnie z powyższym: liczby  ,
, 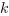 ,
, 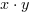 ,
, 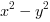 to literały.
Liczby
to literały.
Liczby 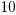 ,
, 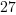 to dane.
to dane.
Liczby rzeczywiste
Liczby, jakie zwykle spotykamy podczas rozwiązywania matemtycznych problemów, to liczby rzeczywiste. Każda liczba rzeczywista może być sklasyfikowana jako dodatnia, ujemna bądź jako zero.
Oś liczbowa
Aby łatwiej zrozumieć własności liczb rzeczywistych, możemy przedstawić je jako punkty na linii prostej. Taką linię nazywamy osią liczbową.
Oś liczbowa jest obustronnie nieskończona. Jeden z punktów jest specjalnie wybrany i określony jako zero.
Aby znaleźć punkt reprezentujący daną liczbę  , należy wybrać jednostkę i
za jej pomocą odmierzyć odległość
, należy wybrać jednostkę i
za jej pomocą odmierzyć odległość  od punktu oznaczonego jako zero. Punkty
po prawej stronie punktu zero oznaczają wartości dodanie. Punkty po lewej stronie
punktu zero oznaczają wartości ujemne.
od punktu oznaczonego jako zero. Punkty
po prawej stronie punktu zero oznaczają wartości dodanie. Punkty po lewej stronie
punktu zero oznaczają wartości ujemne.
Mówimy, że liczba  jest większa od liczby
jest większa od liczby 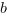 ,
jeżeli punkt reprezentujący liczbę
,
jeżeli punkt reprezentujący liczbę  leży na osi liczbowej na prawo od punktu
reprezentującego liczbę
leży na osi liczbowej na prawo od punktu
reprezentującego liczbę 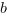 . W przeciwnym wypadku mówimy, że
. W przeciwnym wypadku mówimy, że  jest
mniejsze od
jest
mniejsze od 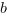 . Zauważmy, że dla liczb ujemnych oznacza to, że np.
. Zauważmy, że dla liczb ujemnych oznacza to, że np. 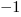 jest większe od
jest większe od 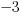 . Fakt, że
. Fakt, że  jest większe od
jest większe od 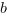 , zapisujemy symbolicznie
jako
, zapisujemy symbolicznie
jako , natomiast
 jest mniejsze od
jest mniejsze od 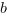 zapisujemy
zapisujemy .
Wartość bezwzględna
Niech 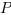 będzie punktem na osi liczbowej reprezentującym liczbę
będzie punktem na osi liczbowej reprezentującym liczbę  , a punkt
, a punkt
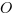 będzie punktem reprezentującym zero. Długość odcinka
będzie punktem reprezentującym zero. Długość odcinka 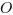
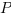 zawsze będzie
liczbą dodatnią, niezależnie od tego, czy liczba
zawsze będzie
liczbą dodatnią, niezależnie od tego, czy liczba  jest dodatnia, czy ujemna.
Długość wspomnianego odcinka jest nazywana wartością bezwzględną liczby
jest dodatnia, czy ujemna.
Długość wspomnianego odcinka jest nazywana wartością bezwzględną liczby  .
.
Wartość bezwzględną liczby  zapisujemy w następujący sposób:
zapisujemy w następujący sposób: 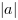 .
.
Zauważmy, że jeżeli  jest liczbą dodatnią, wtedy
jest liczbą dodatnią, wtedy 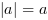 , ale jeżeli
, ale jeżeli  jest ujemne, wtedy
jest ujemne, wtedy 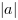 jest równe wartości
jest równe wartości  ze zmienionym znakiem.
ze zmienionym znakiem.
Przykładowo: 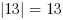 ,
, 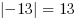 ,
, 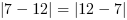 =
=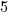 .
.
Chcę wiedzieć więcej na temat: wartość bezwzględna