Równanie kwadratowe

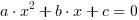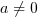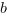Równanie, które może być zapisane w postaci , gdzie oraz , i 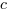nie są zależne od , nazywamy równaniem kwadratowym zmiennej . Dziedziną równania kwadratowego jest zbiór liczb rzeczywistych.

Powyższa postać równania kwadratowego jest nazywana postacią ogólną. Często istnieje konieczność doprowadzenia równania do postaci ogólnej przedstawionej powyżej.

Przykład Doprowadź do postaci ogólnej rówanie
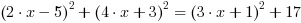
Podnosimy zawartości nazwiasów do kwadratu:

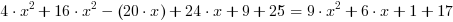
Redukujemy wyrazy podobne, przenosimy wszystko na lewą stroę równania i otrzymujemy:

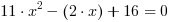
Rozwiązanie równania kwadratowego

Rozwiążemy teraz równanie kwadratowe w sposób ogólny.
Niech: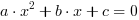
Przenosimy na prawo wyraz stały: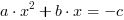
Dzielimy przez :
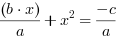
Do obu stron dodajemy :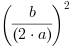
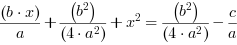
Kożystamy z wzoru skróconego mnożenia: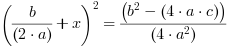
Wyciągamy pierwiastek: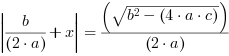

Po zdjęciu wartości bezwzględnej są dwie możliwości:

1. , czyli:
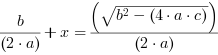2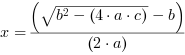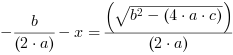. , czyli: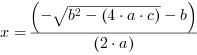

Ostateczenie wzory na pierwiastki równania kwadratowego to:
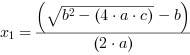i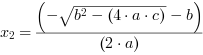

Wyróżnik delta

Dla uproszczenia wzorów na pierwiastki równania kwadratowego wprowadzono wyróżnik delta równy:

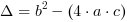
Wzory na pierwiastki równania kwadratowego z wykorzystaniem delty przyjmują następującą postać:
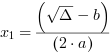i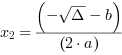

Od wyróżnika zależy również liczba miejsc zerowych funkcji kwadratowej 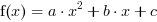(liczba pierwiastków trójmianu kwadratowego, liczba rzeczywistych rozwiązań równania ):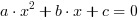

• jeżeli 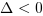, to funkcja kwadratowa nie ma miejsc zerowych,
• jeżeli 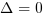, to funkcja kwadratowa ma dokładnie jedno miejsce zerowe: ,
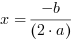• jeżeli 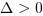, to funkcja kwadratowa ma dwa miejsca zerowe: 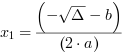i ,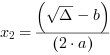

Postać iloczynowa równania kwadratowego

Jeżeli 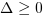, to równanie kwadratowe można doprowadzić do postaci iloczynowej:

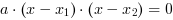
Wzory Viete'a

Jeżeli 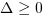, wtedy pierwiastki równania kwadratowego spełniają następujące wzory: 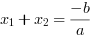i .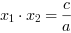

Postać kanoniczna równania kwadratowego

Równanie kwadratowe można doprowadzić do postaci kanonicznej:

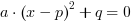, gdzie , , .

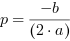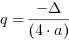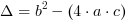Wykres funkcji kwadratowej

Wykresem funkcji kwadratowej jest parabola o wierzchołku w punkcie o wspórzędnych (, ).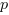

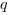Ramiona paraboli skierowane są do góry, gdy 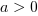, do dołu, gdy .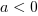