zamiana na ułamek dziesiętny lub zwykły
Wypróbuj też:
Tutaj możesz zobaczyć działania prowadzące do zamiany ułamka na ułamek dziesiętny, lub
zamiany ułamka dziesiętnego na zwykły.
Podaj licznik i mianownik ułamka zwykłego lub cyfry ułamka dziesiętnego a następnie wciśnij przycisk Oblicz.
Porada: Licznik i mianownik muszą być liczbami całkowitymi. Jeżeli w ułamku dziesiętnym chcesz zapisać rozwinięcie nieskończone użyj nawiasu, np. 0,(6) oznacza
nieskończoną ilość szóstek po przecinku (tzw. ułamek okresowy).
Jak to się robi?
Zamiana ułamka zwykłego na dziesiętny
Aby zamienić ułamek zwykły na dziesiętny wystarczy podzielić licznik przez mianownik.
Przykład
Chcemy zamienić na postać dziesiętną ułamek . Dzielimy więc 3 przez 4 i uzyskujemy
liczbę 0,75 która jest poszukiwaną postacią dziesiętną.
. Dzielimy więc 3 przez 4 i uzyskujemy
liczbę 0,75 która jest poszukiwaną postacią dziesiętną.
Zamiana ułamka dzisiętnego na zwykły
Jeżeli ułamek nie jest okresowy wtedy wystarczy zapisać cyfry po przecinku jako licznik a jako mianownik liczbę mającą na początku cyfrę 1 a później tyle zer ile jest cyfr w liczniku. Jeżeli w wyjściowym ułamku są jakieś cyfry przed przecinkiem wtedy do licznika ułamka zwykłego należy jeszcze dodać liczbę składającą się z cyfr znajdujących się przed przecinkiem przemnożoną przez wartość mianownika. Jeżeli można należy jeszcze taki ułamek skrócić, aby uzyskać jak najprostszą postać.
Przykład
Chcemy zamienić 3,72 na ułamek zwykły. Licznikiem będzie liczba 72. Mianownik będzie miał na początku 1 i dwa zera (bo są dwie cyfry po przecinku), czyli będzie liczbą 100. Mamy na razie ułamek: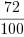 , który po skróceniu
byłby naszym wynikiem gdyby przed przecinkiem była tylko cyfra 0. W tym wypadku musimy jeszcze do licznika dodać liczbę złożoną z cyfr
przed przecinkiem (3) przemnożoną przez mianownik (100). Uzyskujemy więc ostateczny licznik jako: 72 + 3 * 100 = 372 i ułamek:
, który po skróceniu
byłby naszym wynikiem gdyby przed przecinkiem była tylko cyfra 0. W tym wypadku musimy jeszcze do licznika dodać liczbę złożoną z cyfr
przed przecinkiem (3) przemnożoną przez mianownik (100). Uzyskujemy więc ostateczny licznik jako: 72 + 3 * 100 = 372 i ułamek:
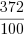 , który możemy jeszcze skrócić dzieląc licznik i mianownik przez 4. Mamy wtedy ostateczny
wynik:
, który możemy jeszcze skrócić dzieląc licznik i mianownik przez 4. Mamy wtedy ostateczny
wynik: 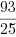 .
.
Zamiana ułamka dzisiętnego okresowego na zwykły
Chcemy zamienić ułamek okresowy 3,7(21) na ułamek zwykły. Oznaczmy tą liczbę jako . Mamy równanie
. Mamy równanie
 = 3,7(21). Teraz musimy pomnożyć to równanie przez taką liczbę, aby "wyjąć"
jedno wystąpie okresu. W tym przypadku musimy pomnożyć przez 100, co daje:
= 3,7(21). Teraz musimy pomnożyć to równanie przez taką liczbę, aby "wyjąć"
jedno wystąpie okresu. W tym przypadku musimy pomnożyć przez 100, co daje:
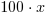 = 372,1(21). Następnie od obu stron równania odejmujemy
= 372,1(21). Następnie od obu stron równania odejmujemy  .
Uzyskujemy:
.
Uzyskujemy: 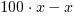 = 372.1(21) - 3.7(21) i po wykonaniu odejmowań:
= 372.1(21) - 3.7(21) i po wykonaniu odejmowań:
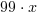 = 368.4. Zauważmy, że redukcji po prawej stronie równaniu uległa część okresowa ułamka
dziesiętnego. Prawą stronę możemy teraz bez większego trudu zamienić na ułamek zwykły
= 368.4. Zauważmy, że redukcji po prawej stronie równaniu uległa część okresowa ułamka
dziesiętnego. Prawą stronę możemy teraz bez większego trudu zamienić na ułamek zwykły 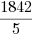 ,
który jeszcze trzeba podzielić przez 99. W ten sposób wyznaczamy
,
który jeszcze trzeba podzielić przez 99. W ten sposób wyznaczamy  z rówania jako ułamek:
z rówania jako ułamek:
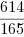 , który jest szukaną postacią liczby 3,7(21).
, który jest szukaną postacią liczby 3,7(21).
Aby zamienić ułamek zwykły na dziesiętny wystarczy podzielić licznik przez mianownik.
Przykład
Chcemy zamienić na postać dziesiętną ułamek
 . Dzielimy więc 3 przez 4 i uzyskujemy
liczbę 0,75 która jest poszukiwaną postacią dziesiętną.
. Dzielimy więc 3 przez 4 i uzyskujemy
liczbę 0,75 która jest poszukiwaną postacią dziesiętną.Zamiana ułamka dzisiętnego na zwykły
Jeżeli ułamek nie jest okresowy wtedy wystarczy zapisać cyfry po przecinku jako licznik a jako mianownik liczbę mającą na początku cyfrę 1 a później tyle zer ile jest cyfr w liczniku. Jeżeli w wyjściowym ułamku są jakieś cyfry przed przecinkiem wtedy do licznika ułamka zwykłego należy jeszcze dodać liczbę składającą się z cyfr znajdujących się przed przecinkiem przemnożoną przez wartość mianownika. Jeżeli można należy jeszcze taki ułamek skrócić, aby uzyskać jak najprostszą postać.
Przykład
Chcemy zamienić 3,72 na ułamek zwykły. Licznikiem będzie liczba 72. Mianownik będzie miał na początku 1 i dwa zera (bo są dwie cyfry po przecinku), czyli będzie liczbą 100. Mamy na razie ułamek:
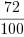 , który po skróceniu
byłby naszym wynikiem gdyby przed przecinkiem była tylko cyfra 0. W tym wypadku musimy jeszcze do licznika dodać liczbę złożoną z cyfr
przed przecinkiem (3) przemnożoną przez mianownik (100). Uzyskujemy więc ostateczny licznik jako: 72 + 3 * 100 = 372 i ułamek:
, który po skróceniu
byłby naszym wynikiem gdyby przed przecinkiem była tylko cyfra 0. W tym wypadku musimy jeszcze do licznika dodać liczbę złożoną z cyfr
przed przecinkiem (3) przemnożoną przez mianownik (100). Uzyskujemy więc ostateczny licznik jako: 72 + 3 * 100 = 372 i ułamek:
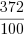 , który możemy jeszcze skrócić dzieląc licznik i mianownik przez 4. Mamy wtedy ostateczny
wynik:
, który możemy jeszcze skrócić dzieląc licznik i mianownik przez 4. Mamy wtedy ostateczny
wynik: 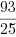 .
.
Zamiana ułamka dzisiętnego okresowego na zwykły
Chcemy zamienić ułamek okresowy 3,7(21) na ułamek zwykły. Oznaczmy tą liczbę jako
 . Mamy równanie
. Mamy równanie
 = 3,7(21). Teraz musimy pomnożyć to równanie przez taką liczbę, aby "wyjąć"
jedno wystąpie okresu. W tym przypadku musimy pomnożyć przez 100, co daje:
= 3,7(21). Teraz musimy pomnożyć to równanie przez taką liczbę, aby "wyjąć"
jedno wystąpie okresu. W tym przypadku musimy pomnożyć przez 100, co daje:
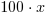 = 372,1(21). Następnie od obu stron równania odejmujemy
= 372,1(21). Następnie od obu stron równania odejmujemy  .
Uzyskujemy:
.
Uzyskujemy: 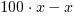 = 372.1(21) - 3.7(21) i po wykonaniu odejmowań:
= 372.1(21) - 3.7(21) i po wykonaniu odejmowań:
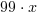 = 368.4. Zauważmy, że redukcji po prawej stronie równaniu uległa część okresowa ułamka
dziesiętnego. Prawą stronę możemy teraz bez większego trudu zamienić na ułamek zwykły
= 368.4. Zauważmy, że redukcji po prawej stronie równaniu uległa część okresowa ułamka
dziesiętnego. Prawą stronę możemy teraz bez większego trudu zamienić na ułamek zwykły 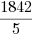 ,
który jeszcze trzeba podzielić przez 99. W ten sposób wyznaczamy
,
który jeszcze trzeba podzielić przez 99. W ten sposób wyznaczamy  z rówania jako ułamek:
z rówania jako ułamek:
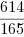 , który jest szukaną postacią liczby 3,7(21).
, który jest szukaną postacią liczby 3,7(21).