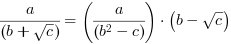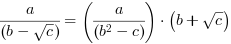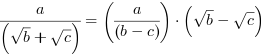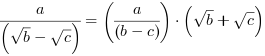Potęgi i pierwiastki
Narzędzia
Potęgi
Dla liczby rzeczywistej  i naturalnej
i naturalnej 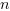 :
:
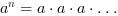 (
(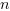 razy)
razy)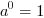 - dla
- dla 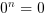 - dla
- dla 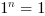
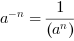 - dla
- dla 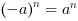 - dla
- dla 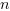 parzystego
parzystego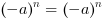 - dla
- dla 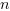 nieparzystego
nieparzystego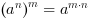
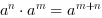
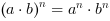
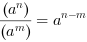
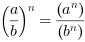
Pierwiastki
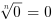
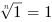
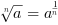
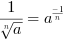 dla
dla 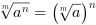 =
=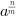
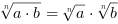
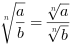
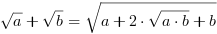 dla
dla i
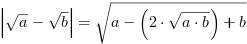 dla
dla i
Usuwanie niewymierności z mianownika
Narzędzia
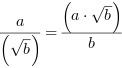
![a/{root[n][b]}=(a*{root[n][b^(n-1)]})/b](/public/formulas/s3-30.png)