Układ równań liniowych
Równanie liniowe dwóch zmiennych
Równanie postaci , gdzie
,
, jest nazywane równaniem
pierwszego stopnia lub równaniem liniowym (ponieważ wykres tego równania jest linią
prostą) zmiennych
 i
i 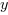 .
.
Załóżmy, że mamy dwa takie równania:
,
Szukamy takiej pary liczb  i
i 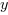 , że oba równania będą prawdziwe po wstawieniu w nie
tych liczb.
, że oba równania będą prawdziwe po wstawieniu w nie
tych liczb.
Metoda przeciwstawnych współczynników
Rozwiązywanie układu równań liniowych metodą przeciwstawnych współczynników polega na pomnożeniu obu równań przez takie liczby, aby współczynniki przy jednej ze zmiennych były równe w obu równaniach lub były równe co do wartości bezwzględnej, ale miały przeciwne znaki. Następnie dodając (w przypadku przeciwnych znaków) lub odejmując (w przypadku takich samych znaków) od siebie oba równania, uzyskujemy równanie, w którym ta zmienna już nie występuje.
O zmiennej, która nie występuje w uzyskanym równaniu mówimy, że została wyeliminowana.
Przykład rozwiąż układ równań:
Staramy się doprowadzić oba równania do postaci, w których współczynniki przy zmiennej  będą
równe. Pierwsze równanie pomnożmy przez
będą
równe. Pierwsze równanie pomnożmy przez , a drugie przez
. Daje to:
Teraz możemy odjąć pierwsze równanie od drugiego, co doprowadzi do eliminacji zmiennej  :
:
Podstawiamy uzyskaną wartość zmiennej 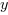 do pierwszego równania:
do pierwszego równania:
Otrzymujemy ostatecznie rozwiązanie układu równań: 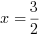 i
i .
Metoda podstawiania
Rozwiązywanie układu równań liniowych metodą podstawiania polega na takim przekształceniu jednego z równań, aby uzyskać wartość jednej ze zmiennych w zależności od drugiej zmiennej. Następnie uzyskaną wartość podstawiamy do drugiego z równań.
Przykład Rozwiąż układ równań:
Przekształacamy pierwsze z równań tak, aby uzyskać  w zależności od
w zależności od 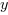 :
:
Teraz uzyskaną wartość podstawiamy do drugiego równania:
Otrzymaną wartość wstawiamy do wyliczonej wartości zmiennej
 od zmiennej
od zmiennej 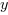 .
Otrzymujemy:
.
Otrzymujemy:
Uzyskujemy ostatecznie rozwiązanie układu równań: i
.
Układ nieoznaczony
Jeżeli jedno z równań układu da się doprowadzić do postaci drugiego równania układu, wtedy taki układ nazywamy układem nieoznaczonym. Układ nieoznaczony ma nieskończenie wiele rozwiązań. Ilustracją graficzną takiego układu będą dwie linie pokrywające się.
Układ sprzeczny
Jeżeli układ nie ma rozwiązań, wtedy taki układ nazywamy układem sprzecznym. Ilustaracją graficzną układu sprzecznego są dwie linie równoległe.