Wartość bezwzględna

Wartość bezwzględną liczby rzeczywistej definiujemy wzorem:

,

co oznacza, że określa ona, jak liczba jest "duża", bez względu na jej znak. Graficznie wartość bezwzględną można przedstawić jako odległość danej liczby na osi liczbowej od punktu 0.

Prawdziwe są zatem następujące zdania:

1. Wartość bezwzględna (odległość) zawsze jest nieujemna:
2. Wartość bezwzględna (odległość) liczby dodatniej od punktu 0 jest taka sama jak odpowiadającej jej liczby ujemnej:

Dla dowolnych liczb , 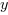mamy:

Ponadto, jeżeli 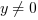, to

oznacza odległość liczby od liczby .

Jeżeli , wtedy możemy analogicznie stwierdzić, że oznacza odległość liczby od liczby .

W związku z powyższym dla dowolnych liczb oraz spełnione są:

• <=> i
• <=> lub

Równanie z wartością bezwzględną

Kiedy rozwiązujemy równanie bądź nierówność, w której występuje wartość bezwzględna, pierwszym krokiem powinno być jej zdjęcie.

Przykład Rozwiąż równanie:
Gdyby chcieć zilustrować to zadanie, moglibyśmy je zastąpić pytaniem, jaka liczba jest odległa od liczby 1 o 3 jednostki.