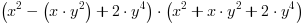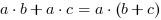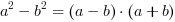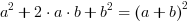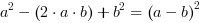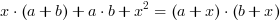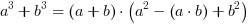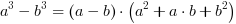Rozkład na czynniki
Wzory skróconego mnożenia
Poniższe mnożenia występują tak często podczas rozwiązywania zadań, że powinny być zapamiętane:
Rozkład na czynniki przez spostrzeżenie
Jeżeli wielomian jest w postaci zgodnej z jednym z powyższych wzorów, może on być rozłożony na czynniki poprzez spostrzeżenie.
Przykład 1. Rozłóż na czynniki wielomian 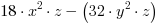 .
.
Z wzoru 1: 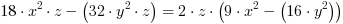
Z wzoru 2: 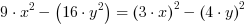 =
=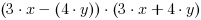
Czyli ostatecznie: 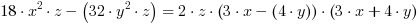
Przykład 2. Rozłóż na czynniki wielomian 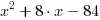
Możemy zastosować wzór 5, jeżeli znajdziemy takie dwie liczby  i
i 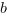 ,
że
,
że 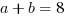 i
i 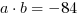 . Zauważamy, że warunek jest
spełniony dla
. Zauważamy, że warunek jest
spełniony dla 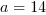 i
i 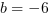 , więc:
, więc: 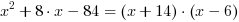 .
.
Przykład 3. Rozłóż na czynniki wielomian 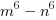
Z wzorów 2, 6 i 7 mamy:
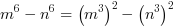 =
=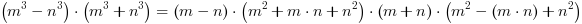
Rozkład na czynniki przez grupowanie
Wiele wyrażeń trudno dopasować do przedstawionych wzorów, jednak da się je doprowadzić do postaci, w której zastosowanie omawianych wzorów jest możliwe. Robi się to poprzez grupowanie wyrazów wielomianu, czyli taką zmianę ich kolejności, aby można było wyciągnąć odpowiednie współczynniki przed nawias. Wyciągane przed nawias współczynniki trzeba tak dobrać, aby po operacji wielomian przybrał postać umożliwiającą zastosowanie wzorów skróconego mnożenia.
Przykład 1. Rozłóż na czynniki wielomian 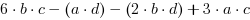 .
.
Po zmianie kolejności mamy: 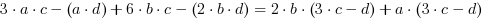 .
.
Teraz możemy już zastosować wzór 1, uzyskując: 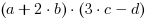 .
.
Przykład 2. Rozłóż na czynniki wielomian 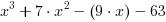 .
.
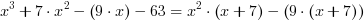 =
=
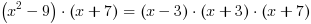
Czasami, żeby zastosować omawianą metodę, należy dodać lub odjąć jeden bądź więcej wyrazów.
Przykład 3. Rozłóż na czynniki wielomian 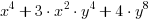
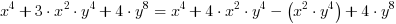 (dodaliśmy i odjęliśmy wyraz
(dodaliśmy i odjęliśmy wyraz 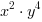 )
)
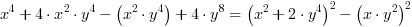 =
=